Copyright (c) 1995-2003, Junzo SATO. All rights reserved.

Pangea

[Graphics:HTMLFiles/index_1.gif]

[Graphics:HTMLFiles/index_2.gif]

Junzo SATO

July 27th 2003

•Introduction

As the reader can see in the reference[1], constuction of the fractal surface is done with simple operations. Cutting the sphere randomly into two hemispheres and adding a random gaussian displacement in radial direction to one of hemispheres give the fractal planet after iterations.

•Great Circle

Assuming that the sphere has an unit radius, the point on the surface is described as follows.

In[1]:=

p = {x, y, z}

Out[1]=

{x, y, z}

The size of the vector should be the unit length.

In[2]:=

p . p == 1

Out[2]=

x^2 + y^2 + z^2 == 1

By introducing an angle η for x-y plane, the above expression is modified.

In[3]:=

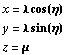
x = λ cos(η) y = λ sin(η) z = μ

Out[3]=

λ Cos[η]

Out[4]=

λ Sin[η]

Out[5]=

μ

Then, the constraint becomes the following.

In[6]:=

p . p == 1

Out[6]=

μ^2 + λ^2 Cos[η]^2 + λ^2 Sin[η]^2 == 1

In[7]:=

% // Simplify

Out[7]=

λ^2 + μ^2 == 1

When we choose a point on the sphere, a great circle, i.e., the edge of the hemisphere is uniquely defined by regarding the specified point as elements of the normal vector of the circle's plane.

In[8]:=

n = {nx, ny, nz}

Out[8]=

{nx, ny, nz}

In[9]:=

p . n == 0

Out[9]=

nz μ + nx λ Cos[η] + ny λ Sin[η] == 0

The normal vector itself should have unit length.

In[10]:=

n . n == 1

Out[10]=

nx^2 + ny^2 + nz^2 == 1

The constraint for the point p is same as the previous one.

In[11]:=

Simplify[p . p == 1]

Out[11]=

λ^2 + μ^2 == 1

Now we can achieve the great circle's coordinates by solving equations for λ and μ.

In[12]:=

s = Simplify[Solve[{p . n == 0, Simplify[p . p == 1]}, {λ, μ}]]

Out[12]=

{{μ -> (-nx Cos[η] - ny Sin[η])/(nz^2 + nx^2 Cos[η]^2 + ny^2 Sin[η ... ), λ -> -nz/(nz^2 + nx^2 Cos[η]^2 + ny^2 Sin[η]^2 + nx ny Sin[2 η])^(1/2)}}

The values λ and μ are determined by η.  Let's define the module which returns a random point on the unit circle.

In[13]:=

r := Module[{ϕ = Random[Real, {0, 2 π}], z = Random[Real, {-1, 1}]}, {(1 - z^2)^(1/2) cos(ϕ), (1 - z^2)^(1/2) sin(ϕ), z}]

This is useful to specify a random normal vector of a great circle.

In[14]:=

l = Map[Apply[Rule, #] &, Transpose[{n, r}]]

Out[14]=

{nx -> -0.06706633303112111`, ny -> 0.36799277876951775`, nz -> -0.92740682645064`}

For example, the first solution of μ with specified vector n becomes the following.

In[15]:=

s[[1, 1, 2]] /. l

Out[15]=

(0.06706633303112111` Cos[η] - 0.36799277876951775` Sin[η])/(0.8600834217472475` + ... 6` Cos[η]^2 + 0.13541868522651124` Sin[η]^2 - 0.024679926254004152` Sin[2 η])^(1/2)

Because it is possible to represent λ and μ as sin(θ) and cos(θ) respectively, we have four plots of η versus θ curve.

In[16]:=

Plot[cos^(-1)(s [[ 1, 1, 2 ]]) /. l, {η, 0, 2 π}, AxesLabel -> {"η&quo ... 2, 2 ]]) /. l, {η, 0, 2 π}, AxesLabel -> {"η", "θ"}]

[Graphics:HTMLFiles/index_32.gif]

Out[16]=

-Graphics -

[Graphics:HTMLFiles/index_34.gif]

Out[17]=

-Graphics -

[Graphics:HTMLFiles/index_36.gif]

Out[18]=

-Graphics -

[Graphics:HTMLFiles/index_38.gif]

Out[19]=

-Graphics -

We can define the θ(rx, ry, rz) using the first solution .

In[20]:=

θ(rx_, ry_, rz_) := cos^(-1)((-rx cos(η) - ry sin(η))/(rz^2 + rx^2 cos^2(η) + ry^2 sin^2(η) + rx ry sin(2 η))^(1/2))

For the special case when the normal vector is along the cartesian ax, this function returns appropriate plots.

In[39]:=

Plot[θ(1, 0, 0), {η, 0, 2 π}] Plot[Chop[θ(0, -1, 0)], {η, 0, 2 π}, PlotRange -> All] Plot[θ(0, 0, 1), {η, 0, 2 π}]

[Graphics:HTMLFiles/index_43.gif]

Out[39]=

-Graphics -

[Graphics:HTMLFiles/index_45.gif]

Out[40]=

-Graphics -

[Graphics:HTMLFiles/index_47.gif]

Out[41]=

-Graphics -

•Random Hemisphere

As the result of the above calculations, the greate circle is defined the following function.

greatcircle(x_, y_, z_) := ParametricPlot3D[ {sin(θ(x, y, z)) cos(η), sin(θ(x, ... -1 1

θplot(x_, y_, z_) := Plot[θ(x, y, z), {η, 0, 2 π}, DisplayFunction -> I ... 0 π

rands = Table[r, {32}] ;

Show[Map[Apply[greatcircle, #] &, rands], DisplayFunction -> $DisplayFunction]

[Graphics:HTMLFiles/index_53.gif]

-Graphics3D -

Show[Map[Apply[θplot, #] &, rands], DisplayFunction -> $DisplayFunction]

[Graphics:HTMLFiles/index_56.gif]

-Graphics -

•Random Cut

The functions of the great circles are obtained.

funcs = Map[Apply[θ, #] &, rands] ;

Let's the counter k to 1.

k = 1 ;

For the k-th function of the great circle, we can get numbers which are rescaled from radian values to degrees.

nums = Table[Round[180 funcs[[k]]/π], {η, 0, 2 π - 2 π/360, 2 π/360}] ;

ListPlot[nums]

[Graphics:HTMLFiles/index_62.gif]

-Graphics -

The matrix of the η - θ plane in degrees is allocated. The size is 360 times 180.

mat = Table[0, {360}, {180}] ;

The package for the normal distribution is loaded.

<< Statistics`NormalDistribution`

Gaussian random number is created using NormalDistribution.

gauss := Random[NormalDistribution[0, 1]]

For the great circle, one of hemispheres is selected randomly. Then the gaussian random number is added to the value of the selected hemisphere.

newcut[nl_] := Module[{g = gauss}, If[Random[] < .5, Join[Table[g, {#}], Table[0, {180 - #}]] & /@ nl, Join[Table[0, {#}], Table[g, {180 - #}]] & /@ nl]]

ListDensityPlot[Reverse[Transpose[newcut[nums]]], Mesh -> False, AspectRatio -> .5]

[Graphics:HTMLFiles/index_69.gif]

-DensityGraphics -

Do[ nums = Table[Round[180 funcs[[k]]/π], {η, 0, 2 π - 2 π/360, 2 π/360}] ; mat = mat + newcut[nums], {k, 1, Length[funcs]}] ;

ListDensityPlot[Reverse[Transpose[mat]], Mesh -> False, AspectRatio -> .5]

[Graphics:HTMLFiles/index_73.gif]

-DensityGraphics -

•Colorization

ConnectRGBColor[{iniR_, iniG_, iniB_}, {finR_, finG_, finB_}, var_] := RGBColor @@ ({iniR, iniG, iniB} (1 - var) + {finR, finG, finB} var)

earthColor[x_] := If[x <= .25, ConnectRGBColor[{0, 0, 0}, {0, 0, 1}, x/.25], If[x <= .65 ... 75) (x - .75)], ConnectRGBColor[{.90, .5, .15}, {.90, .5, .15} * 0.1, 1/(1 - .875) (x - .875)]]]]]

a = Table[{earthColor[i/30.], Rectangle[{i, 0}, {i + 1, 5}]}, {i, 0, 30}] ; Show[Graphics[a], AspectRatio -> Automatic]

[Graphics:HTMLFiles/index_78.gif]

-Graphics -

ListDensityPlot[Reverse[Transpose[mat]], Mesh -> False, AspectRatio -> .5, ColorFunction -> (earthColor[#] &)]

[Graphics:HTMLFiles/index_81.gif]

-DensityGraphics -

max = Max[mat] ; min = Min[mat] ; lvl = Map[(# - min)/(max - min) &, mat, {2}] ;

General :: spell1 : スペル間違いの可能性があります．新規シンボル\" max \"はすでにあるシンボル\" Max \"に似ています．

General :: spell1 : スペル間違いの可能性があります．新規シンボル\" min \"はすでにあるシンボル\" Min \"に似ています．

•Graphics3D

pt[i_, j_] := {Cos[2 Pi i/360] Sin[Pi j/180], Sin[2 Pi i/360] Sin[Pi j/180], Cos[Pi j/180]} // N

pt[360, j_] := pt[0, j]

pangea = Show[Graphics3D[ Join[ Table[{earthColor[lvl[[i + 1, 1]]], EdgeForm[], Polygon[{pt[i, ... orm[], Polygon[{pt[i, 180], pt[i + 1, 179], pt[i, 179]}]}, {i, 0, 359}]], Lighting -> False ]]

[Graphics:HTMLFiles/index_89.gif]

-Graphics3D -

•QuickDraw3D

Using my 3dmf-for-mathematica application package, the graphics object is converted to the QuickDraw3D metafile.

<< QD3D`QuickDraw3D`

Welcome to the shareware package \"3DMF for MATHEMATICA\"!

Exporting Graphics3D and SurfaceGraphics into the QuickDraw3D Metafile format is possible.

Write3DMF["pangea.3dmf", pangea]

pangea.3dmf

The QuickDraw3D Viewer for Windows is available from Apple.

[Graphics:HTMLFiles/index_96.gif]

•LiveGraphics3D

Unfortunately, the LiveGraphics3D doesn't work for the graphics output with large number of polygons.

•Pangea Application

Many years ago, I wrote an application Pangea for the MacOS classic. It works extremely faster than Mathematica because it's written by C++. The following screenshot shows the result of 5000 cutting steps generated about only 10 second.

[Graphics:HTMLFiles/index_97.gif]

•Reference

[1] Roman E. Maeder, "The Mathematica Programmer II", Academic Press, 1996

Converted by Mathematica  (July 28, 2003)